| GISdevelopment.net ---> AARS ---> ACRS 2004 ---> GPS & Photogrammetry: Navigation System |
A Review of Stochastic Models
Used in Static GPS Positioning Technique
Chalermchon
Satirapod
Geo-Image Technology Research Unit
Department of Survey Engineering, Chulalongkorn University, Thailand
Tel. 66-2-2186662 Fax 66-2-218-6653
Email: chalermchon.s@chula.ac.th
Geo-Image Technology Research Unit
Department of Survey Engineering, Chulalongkorn University, Thailand
Tel. 66-2-2186662 Fax 66-2-218-6653
Email: chalermchon.s@chula.ac.th
ABSTRACT
In order to achieve high-accuracy positioning results, GPS carrier phase observations have to be used in the data processing step. It is generally known that there are two important aspects to the optimal processing of GPS observations, the definitions of the so-called functional model and the corresponding stochastic model. The functional model describes the mathematical relationship between the GPS observations and the unknown parameters, while the stochastic model describes the statistics of the GPS observations. The functional model is nowadays sufficiently known, however the definition of the stochastic model still remains a challenging research topic. Data differencing techniques are extensively used for constructing the functional model as they can eliminate many of the troublesome GPS biases, such as the atmospheric bias, the receiver clock bias, the satellite clock bias, and so on. However, some unmodelled biases still remain in the GPS observations following such differencing. The challenge is to find a way to realistically incorporate information on such unmodelled biases into the stochastic model. Recently there has been interest in using three types of data, Signal-to-Noise Ratio, satellite elevation and least-squares residual, as quality indicators for a formulation of the stochastic model. This paper will describe fundamental equations for processing of GPS data and the three quality indicators commonly used for a construction of the stochastic model. A review of the recent development works in stochastic models for static GPS positioning is also given.
1. INTRODUCTION
GPS has been playing an increasingly important role in high-precision surveying and geodetic applications. As with traditional geodetic network adjustment, data processing for precise GPS static positioning is invariably performed using the least-squares method. To employ the least-squares method, both the functional and stochastic models of the GPS measurements need to be defined. The functional model, also called the mathematical model, describes the mathematical relationships between the GPS measurements and the unknown parameters, such as the ambiguity terms and the baseline components. The stochastic model describes the statistical properties of the measurements, which are mainly defined by an appropriate covariance matrix. In order to ensure high accuracy, both the functional model and the stochastic model must be correctly defined. If the function model is adequate, the residuals obtained from the least-squares solution should be randomly distributed (e.g. Tiberius & Kenselaar, 2000; Satirapod et al., 2001a). Over the last two decades the functional models for GPS carrier phases have been investigated in considerable details, and are well documented in the literature (e.g. in such texts as Hofmann-Wellenhof et al., 1997; Leick, 1995; Rizos, 1997). Since GPS measurements are contaminated by many errors such as the atmospheric biases, the receiver clock bias, the satellite clock bias, and so on, it is impossible to model all systematic errors in the functional model without some understanding, or prior knowledge, of the physical phenomena which underpin these errors. The data differencing techniques are extensively used for constructing the functional model. However, some unmodelled (or 'residual') biases still remain in the GPS observations following such differencing. As a result, the residuals obtained from a least-squares static solution would normally represent both unmodelled systematic errors and noise. In principle it is possible to further improve the accuracy and certainty of GPS results through an enhancement of the stochastic model. Many researchers have emphasised the importance of the stochastic model, especially for high-accuracy applications (e.g. Barnes et al., 1998; Han, 1997; Satirapod, 2002; Wang, 1999). The challenge is to find a way to realistically incorporate information on such unmodelled biases into the stochastic model. Therefore, accurate stochastic modelling for the GPS measurements is still both a controversial topic and a difficult task to implement in practice (Cross et al., 1994; Wang et al., 2002). This paper is organised as follows. In section two, fundamental equations for processing of GPS data are explained in details. The three quality indicators commonly used for a construction of the stochastic model are described in section three. The recent stochastic models for static GPS positioning are briefly reviewed in section four. Some concluding remarks and recommendations are given in section five.
2. FUNDAMENTAL EQUATIONS FOR PROCESSING OF GPS DATA
Like other traditional surveying techniques, GPS data processing is normally carried out using the least-squares method. The implementation of the least-squares method requires a set up of both functional and stochastic models. Double-differenced (DD) carrier phase observations are widely used in many GPS software packages as a way to construct the functional model since it efficiently cancels many systematic errors existing in the GPS measurements. For short baseline case, the DD carrier phases can be expressed as
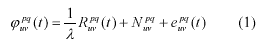
where the superscripts p and q denote satellites, and the subscripts u and v specify the receivers, and the indices t denote the epoch at which the data were collected. R is the geometric distance to the satellites, l is the wavelength of the carrier wave, and N is the DD integer ambiguity. The term e represents all possible errors.
Given that the vector x contains all the unknown parameters necessary for baseline data processing, the standard observation equation for processing of GPS data is:
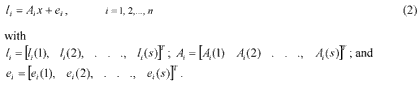
In Equation (2), i l is an 1 ´ s vector of the observed-minus-computed DD carrier phase values; i A is the design matrix corresponding to the measurements i l ; i e is an 1 ´ s vector of the error terms for the measurement i l ; n is the number of satellite pairs forming the DD observations; and s is the number of observation epochs.
In practice, GPS measurements are usually assumed to have the same precision and to be statistically independent in time and space. Subsequently, a covariance matrix for all the DD observations l can be constructed using the error propagation law. In this covariance matrix the correlation coefficient between any two DD measurements is +0.5. This so-called ‘mathematical correlation’ is introduced by the double-differencing process. To set up a simple stochastic model for DD measurements, it is further assumed that temporal correlations are absent.
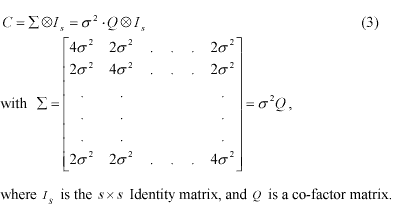
With the functional and stochastic models expressed by equations (2) and (3), the least-squares estimator of the unknowns, and the residuals of the measurements, can be obtained:
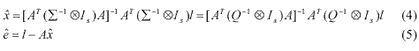
Clearly, the estimator xˆ is independent of the variance factor. The optimal estimate of this variance factor is given by:

3. QUALITY INDICATORS FOR A FORMULATION OF THE STOCHASTIC MODEL
Considering the assumptions underlying a formulation of the stochastic model in equation (3), one can see that these assumptions are not realistic. This is due to the fact that the GPS measurement errors are dominated by the systematic errors caused by the orbit, atmospheric and multipath effects, which are quite different for each satellite. Therefore, the measurements obtained from different satellites cannot have the same precision. On the other hand, the raw measurements are spatially correlated due to similar observing conditions for these measurements (it is this fact that makes the double-differencing procedure effective in mitigating measurement biases). This type of correlation is generally called ‘spatial correlation’. Moreover, the time correlations (or temporal correlations) may exist in the measurements because the residual systematic errors change slowly over time. As previously mentioned, there has recently been interest in using three types of data, satellite elevation, Signal-to-Noise Ratio (SNR) and least-squares residual, as quality indicators for a construction of a more realistic stochastic model. It is therefore important to gain a better understanding of these quality indicators.
3.1 Satellite Elevation
Satellite elevation angle information is often used to construct a modified stochastic model. Basic assumption of using the satellite elevation angle information is that each satellite has a different precision and it is assumed that a low elevation angle satellite tends to be noisier than a high elevation angle satellite. The relationship between satellite elevation angle information and precision can be modelled quite well by an exponential function.
3.2 Signal-to-Noise Ratio (SNR)
Recently, SNR was introduced as a quality indicator for GPS observations and used to construct the stochastic model for high-accuracy applications. Basic assumption is that each satellite has a different precision which is dependent on the SNR information. The satellite that has a high SNR value will be less noisier than the satellite with a low SNR value. Langley (1997) claims that SNR is the key parameter in analysing GPS receiver performance and that it directly affects the precision of GPS observations.
3.3 Least-Squares Residual
Basic assumption is that residuals obtained from the least-squares process would represent the same characteristic as true errors if the observation period is long enough to remove any systematic error. Thus, the precision of each satellite is dependent on the residuals obtained from least-squares process. Based on the use of least-squares residuals, many rigorous statistical methods, i.e. MINQUE (Rao, 1971), Bayes estimation (Ziqiang, 1991) have been used to estimate a more realistic covariance matrix.
4. REVIEW ON RECENT STOCHASTIC MODELS FOR STATIC GPS POSITIONING
As discussed in the third section, the GPS observations obtained from different satellites have the different precision and are spatially and temporally correlated. To model the heteroscedasticity, two types of external information, the SNR and the satellite elevation angle, are used to calculate the precision of the one-way GPS measurements. This is done by employing an approximate formula using the satellite elevation angle (e.g. Gerdan, 1995; Han, 1997; Jin, 1996), or SNR (e.g. Brunner et al., 1999; Langley, 1997; Lau & Mok (1999); Talbot, 1988) as input. Given the variances of the one-way GPS measurements, the covariance matrix for the DD measurements can be easily constructed using the error propagation law. A series of tests were carried out by Satirapod & Wang (2000) to investigate both SNR and satellite elevation angle information. They concluded that in general, both SNR value and satellite elevation angle information can be used as quality indicators, but they do not always reflect reality. In addition, the relationship between these quality indicators and the standard deviations of the GPS observations are largely dependent on the data used in for their derivation, and hence the statistical properties of the estimations are still ambiguous. Fortunately, in the case of static or even rapid static GPS positioning techniques, redundant observations are available, from which realistic variance-covariance matrices can be estimated using modern statistical methods based on the use of least-squares residuals. Therefore, a rigorous statistical method, known as MINQUE, has been proposed by Wang et al. (1998) to estimate a fully populated stochastic model for the GPS DD measurements. However, the computational burden of this method was still a significant limitation, as was the requirement to have an equal number of variance-covariance components in the estimation step. Satirapod et al. (2002) have subsequently derived a simplified MINQUE procedure which the computational load and time are significantly reduced. Furthermore, the effect of a change in the number of tracked satellites on the computation is effectively dealt with. Although the improvement in terms of the reliability and accuracy of positioning results have been demonstrated by the modified stochastic models derived from satellite elevation angle, SNR and least-squares residual information, the temporal correlations are still assumed to be absent in these stochastic models.
The impact of temporal correlations on GPS baseline determination has long been investigated in, for example, El-Rabbany (1994), Han & Rizos (1995), Howind et al. (1999), and Satirapod et al. (2001b). Howind et al. (1999), and Satirapod et al. (2001b) concluded that there are significant effects on the station coordinates and their accuracy estimates when the temporal correlations are taken into account. In these studies all one-way measurements are considered to be independent and having the same variance and same temporal correlation. Since it has been shown that different satellites have different temporal correlation coefficients (Wang, 1999), it is not appropriate to make such assumptions. Recently, the iterative stochastic modelling procedure has been proposed by Wang et al. (2002) in order to efficiently deal with the temporal correlations. The procedure is based on a linear classical least squares process, with the basic idea being to first transform the DD carrier phase measurements into a new set of measurements using estimated temporal correlation coefficients. These transformed measurements are free of time correlations, and thus have a block diagonal covariance matrix. The covariance matrix for the new measurements can be estimated using the MINQUE method (or the simplified MINQUE procedure). However, this procedure assumes that the time series of residuals are stationary and follows the first-order vector auto-regressive model. This procedure is therefore suitable for short observation periods. Based on a development in the iterative stochastic modelling procedure, a segmented stochastic modelling procedure has been introduced by Satirapod et al. (2001b) to effectively deal with long observation periods, and at the same time to reduce the computational load.
5. CONCLUDING REMARKS AND RECOMMENDATIONS
In this paper, fundamental equations for GPS data processing are explained in details and an importance of the stochastic model is emphasized. The three quality indicators, SNR, satellite elevation angle and least-squares residual, used for a construction of the stochastic model are briefly described. The recent development works in stochastic models for static GPS positioning are reviewed. It has been noted that the GPS measurement may have a heteroscedastic, space- and time-correlated error structure (Wang, 1999). Therefore, the iterative stochastic modeling procedure is so far the most complete and rigorous stochastic model used in the static GPS positioning technique since all of the aforementioned error features of GPS measurements are taken into account in this procedure. Based on the author’s experience in development work on the stochastic model, the following recommendations can be made for future research work.
- A characteristic of a time series of least-squares residuals needs to be investigated in detail to determine the best fit model for them.
- An optimal window length to be used in the estimation of the stochastic modelling procedure needs to be investigated. This is to ensure that a robust performance can be achieved.
- Barnes, B.J., Ackroyd, N. and Cross, P.A. (1998) Stochastic modelling for very high precision teal-time kinematic GPS in an engineering environment, FIG XXI International Conference, Brighton, U.K., 21-25 July, Commission 6, pp. 61-76.
- Brunner, F.K., Hartinger, H. and Troyer, L. (1999) GPS signal diffraction modelling: The stochastic SIGMA-D model, Journal of Geodesy, 73, pp. 259-267.
- Cross, P.A., Hawksbee, D.J. and Nicolai, R. (1994) Quality measures for differential GPS positioning, The Hydrographic Journal, 72, pp. 17-22.
- El-Rabbany, A.E-S. (1994) The effect of Physical Correlations on the Ambiguity Resolution and Accuracy Estimation in GPS Differential Positioning, Ph.D. thesis, Department of Geodesy and Geomatics Engineering, University of New Brunswick, Canada, 161pp.
- Gerdan, G.P. (1995) A comparison of four methods of weighting double-difference pseudo-range measurements. Trans Tasman Surveyor, Canberra, Australia, 1, pp. 60-66.
- Han, S. and Rizos, C. (1995) Standarization of the variance-covariance matrix for GPS rapid static positioning, Geomatics Research Australasia, 62, pp. 37-54.
- Han, S. (1997) Quality control issues relating to instantaneous ambiguity resolution for real-time GPS kinematic positioning, Journal of Geodesy, 71, pp. 351-361.
- Hofmann-Wellenhof, B., Lichtenegger, H. and Collins, J. (1997) Global Positioning System: Theory and Practice, 4 th edition, Springer-Verlag, Berlin Heidelberg New York, 389pp. Howind, J., Kutterer, H. and Heck, B. (1999) Impact of temporal correlations on GPS-derived relative point positions, Journal of Geodesy, 73, pp. 246-258.
- Jin, X. (1996) Theory of Carrier Adjusted DGPS Positioning Approach and Some Experimental Results, Ph.D. thesis, Technical University of Delft, The Netherlands, 162pp.
- Langley, R.B. (1997) GPS receiver system noise, GPS World, 8, pp. 40-45.
- Lau, L. and Mok, E. (1999) Improvement of GPS relative positioning accuracy by using SNR, Journal of Surveying Engineering, 125(4), pp. 185-202.
- Leick, A. (1995) GPS Satellite Surveying, 2 nd edition, John Wiley & Sons, Inc., New York, 560pp.
- Rao, C.R. (1971) Estimation of variance and covariance components- MINQUE, Journal of Multivariate Analysis, 1, pp. 257-275.
- Rizos, C. (1997) Principles and Practice of GPS Surveying, Monograph 17, School of Geomatic Engineering, The University of New South Wales, 555pp.
- Satirapod, C. and Wang, J. (2000) Comparing the quality indicators of GPS carrier phase observations, Geomatics Research Australasia, 73, pp. 75-92.
- Satirapod, C., Ogaja, C., Wang, J. and Rizos, C. (2001a) An approach to GPS analysis incorporating wavelet decomposition, Artificial Satellites, 36(2), pp. 27-35.
- Satirapod, C., Wang, J. and Rizos, C. (2001b) A New Stochastic Modelling Procedure for Precise Static GPS Positioning, Zeitschrift für Vermessungswessen, 126(6), pp. 365-373.
- Satirapod C. (2002) Improving the GPS Data Processing Algorithm for Precise Static Relative Positioning, PhD thesis, School of Surveying & Spatial Information Systems, The University of New South Wales, Sydney, Australia, 131pp.
- Satirapod, C., Wang, J. and Rizos, C. (2002) A simplified MINQUE procedure for the estimation of variance-covariance components of GPS observables, Survey Review, 35(286), pp. 582-590.
- Talbot, N. (1988) Optimal weighting of GPS carrier phase observations based on the signal-to-noise ratio, International Symposium on Global Positioning Systems, Brisbane, Australia, October, pp. 4.1-4.17.
- Tiberius, C.C.J.M. and Kenselaar, F. (2000) Estimation of the stochastic model for GPS code and phase observables, Survey Review, 35, pp. 441-454.
- Wang, J, Stewart, M.P. and Tsakiri, M. (1998) Stochastic modelling for static GPS baseline data processing, Journal of Surveying Engineering, 121(4), pp. 171-181.
- Wang, J. (1999) Modelling and Quality Control for Precise GPS and GLONASS Satellite Positioning, Ph.D. thesis, School of Spatial Sciences, Curtin University of Technology, Perth, Australia, 171pp.
- Wang, J., Satirapod, C., and Rizos, C. (2002) Stochastic assessment of GPS carrier phase measurements for precise static relative positioning, Journal of Geodesy, 76(2), pp. 95-104.
- Ziqiang, O. (1991) Approximative bayes estimation for variance components, Manuscripta Geodaetica, 16, pp. 168-172.