| GISdevelopment.net ---> AARS ---> ACRS 2000 ---> Image Processing |
A New Approach for Automatic
Determination of Edge Center Lines in a Digital Image
Jaan-Rong TSAY
Assistant Professor, Department of Surveying Engineering
National Cheng Kung University
1 University Road, Tainan ,Taiwan
Tel: (886)-6-2370876 ext. 838 Fax: (886)-6-2375764
e-mail:tsayjr@mail.ncku.edu.tw
Jaan-Rong TSAY
Assistant Professor, Department of Surveying Engineering
National Cheng Kung University
1 University Road, Tainan ,Taiwan
Tel: (886)-6-2370876 ext. 838 Fax: (886)-6-2375764
e-mail:tsayjr@mail.ncku.edu.tw
Keywords:Digital Image, Edge Center Line, Gradient Operator, Wavelets, Zero-Crossing
Abstract
Firstly, this paper proposes a set of new symmetric gradient operators. They were derived from the wavelet theory and some well-known compactly supported orthonormal wavelets. Some tests are done using digital images. They conclude that such operators are really better edge-detectors e.g. than the Sobel ones. Secondly, a new approach for automatic determination of edge center lines in a digital image is presented. It integrates these new wavelet-based gradient operators with the general zero-crossing principle. Test results show apparently that it can automatically determine all center edge-lines of one pixel width.
1. Introduction
At present, edge features are often used in different kinds of image-based techniques, e.g. photogrammetry, remote sensing, computer vision, image understanding and so on. Based on those edge features, geometrical, physical-radiometric and semantic data and information as well can be extracted semi- or even full-automatically by different algorithms, where digital or digitized images are the main input data. In the field of image processing, there are already many different kinds of operators and methods for detecting three basic types of discontinuities: points, lines, and edges. For detail, please see e.g. (Gonzalez and Woods, 1993). In this paper, an alternative new method for automatic edge detection in an image is presented.
The section 2 describes briefly the mathematical derivation and presents a set of new gradient operators. Some tests and analyses are also given there. In section 3, a new approach for automatic determination of edge center lines is given. Some preliminary test results are analyzed in section 4. Conclusions are made in section 5.
2. A Set Of New Gradient Operators
2.1 Brief Depiction on Mathematical Derivations
If a signal f exists in a so-called Hilbert space, it can be represented in a linear form based on orthonormal bases. For instance, the space of square-summable sequences and the space of square-integrable functions depicted in (Vetterli and Kovacevic, 1995) are two examples of the so-called Hilbert spaces. The compactly supported Daubechies wavelets proposed in (Daubechies, 1988) are examples of orthonormal bases. The theory for multiresolution signal decomposition was firstly presented in (Mallat, 1989). It was derived based on those signals f in a Hilbert space. The signal component Ajf of f in a resolution space Vj is so defined that it has the property of minimal error energy, i.e. ò (Ajf(t)-f(t))2 dt is minimal. Herewith, all coefficients in the linear representation are defined. Ajf can be further decomposed into two orthogonal components Aj-1f and Dj-1f. They exist in two Vj 's subsets. One is a coarser resolution space Vj-1 than Vj . The other one is the orthogonal complement of Vj-1 in Vj. It is a so-called wavelet space and denoted by Oj-1. On all equidistant dyadic grid points stated in (Rioul and Duhamel, 1992; Jawerth and Sweldens, 1994), the decomposition derives the basic mathematical formulas of image decomposition shown in (Mallat, 1989). (Tsay, 1996) gave a more user-friendly formulas for image decomposition and image reconstruction. If the first derivatives of those wavelet bases used in that decomposition exist, a new gradient operator can be derived from the derivative values on all dyadic grid points. In case that Daubechies wavelets are used, these operators are defined as follows (Tsay, 1998):
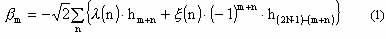
where bm is the m-th element of the operator; hk is the k-th low-pass filter coefficient of the Daubechies wavelet;
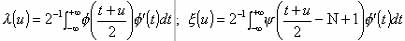
; N is the order of Daubechies wavelets; f and y are the father and mother wavelet of Daubechies, respectively. Table 1 shows the new gradient operators derived from the Daubechies wavelets of order N = 3 (1) 10. These new gradient operators are to be named as "Daubechies operators" in this paper.
2.2 New Symmetrical Gradient Operators
Apparently, they are symmetrical gradient operators. Moreover, it is verified that the operators determined by the asymmetric Daubechies wavelets are the same with the ones determined by the least asymmetric Daubechies wavelets of the same order N.
Table 1. New gradient operators derived from the Daubechies wavelets of order N = 3 (1) 10, where b0=0 and the other bm -coefficients are equal to zero (|m|>2N+1) or they are insignificant coefficients with |bm|<10-6 ( |m|£2N+1).
| m | bm=-b-m | m | bm=-b-m | |||
| N=3 | 1 2 3 4 |
0.745205 -0.145205 0.014612 0.000342 |
N=7 | 1 2 3 4 5 6 7 8 |
0.868744 -0.282965 0.090189 -0.022687 0.003881 -0.000337 -0.000004 0.000002 | |
| N=4 | 1 2 3 4 5 6 |
0.793010 -0.191999 0.033580 -0.002224 -0.000172 0.000001 |
N=8 | 1 2 3 4 5 6 7 |
0.883446 -0.303259 0.106364 -0.031290 0.006958 -0.001032 0.000077 | |
| N=5 | 1 2 3 4 5 6 |
0.825906 -0.228820 0.053353 -0.007461 0.000239 0.000054 |
N=9 | 1 2 3 4 5 6 7 8 |
0.895316 -0.320312 0.120954 -0.039953 0.010617 -0.002103 0.000278 -0.000020 | |
| N=6 | 1 2 3 4 5 6 7 |
0.850137 -0.258553 0.072441 -0.014546 0.001589 -0.000004 -0.000012 |
N=10 | 1 2 3 4 5 6 7 8 9 |
0.905071 -0.334784 0.134055 -0.048427 0.014669 -0.003526 0.000631 -0.000077 0.000005 |
2.3 Test Results
Figure 1 shows an image of the national monument "Anping Fort" in Tainan, Taiwan, and its gradient images computed by the Sobel operators (Gonzalez and Woods, 1993) and by the Daubechies operators of order N=3 and N=10, respectively. In the same manner as common practice, the gradient is approximated with absolute values (Gonzalez and Woods, 1993). In all computations of gradients, all operators are normalized so that åbm=1. Figure 2 expresses the mean, RMS (=root mean square) value, and maximum of gradients of the "Anping Fort" image. Apparently, the gradients computed by the Daubechies operators of N=3 (1) 10 have larger mean, RMS and maximal gradients than the ones determined by the Sobel operators. There exists a distinct effect. For example, Figure 3 illustrates an image of a Chinese character 'dragon' and its gradient images. Daubechies operators can extract much finer edges than the Sobel operators. Moreover, the center lines of all edges determined by both Daubechies and Sobel operators are the same. Figure 4 illustrates an example. The edges computed by the Daubechies operator of order N=3 are located in the centers of the edges computed by the Sobel operators.
In other words, the proposed Daubechies operators are new ones for gradient computation. Test results show that they can extract unbiased and finer edges, e.g. than the Sobel operators.
 | |
| (a) | (b) |
 | |
| (c) | (d) |
Figure 1. (a) an image of Anping Fort in Tainan, Taiwan, and its gradient images computed by the Sobel operators (b), the Daubechies operator of order N=3 (c) and N=10 (d), respectively.
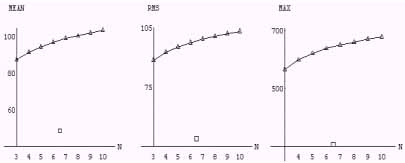
Figure 2. mean values (left), RMS (middle) and maximum (right) of gradients of the "Anping Fort" image shown in Figure 1 computed by the Daubechies operator of N = 3 (1) 10, where the square denotes the ones determined by the Sobel operators.
 | |||
| (a) | (b) | (c) | (d) |
Figure 3. (a) an image of a Chinese character "dragon" and its gradient images computed by the Sobel operator (b), Daubechies operators of N=3 (c) and N=10 (d), respectively.

Figure 4. The edges computed by the Daubechies operator of order N=3 (white center lines) are located in the center of the edges computed by the Sobel operators (dark boundary lines).
3. A New Approach for Automatic Determination of Edge Center Lines
The above-mentioned superior characteristics of the Daubechies operators are further integrated with the principle of zero-crossing for a much more effective edge detection. A new approach for automatic determination of edge centers is thus developed.
| Input image data
Compute the estimation of image noise Wavelet-Based Low-Pass Filtering, if it is needed Select a Daubechies operator of order N Compute the first derivatives G' by the Daubechies operator Compute the second derivatives G" by the Daubechies operator with respect to G' Locate each edge by zero-crossing of second derivatives Linking edge pixels Output all extracted edges |
Figure 5. A new algorithm for automatic determination of edge center lines in an image.
In the next steps, the first derivatives G' are computed by the Daubechies operators. Then, the second derivatives G" are computed by the same Daubechies operators but with respect to the first derivatives G'. Now, each edge is automatically detected by zero-crossing of the second derivatives. All pixels are detected as a pixel on an edge and are denoted as black pixels, abbreviated as B-pixels, if the following conditions exist:
(if G' > s0 and G" decreases from positive to negative numbers) or
(if G' < s0 and G" increases from negative to positive numbers) (2)
where s0 is a positive real number. Until now, all test results show that the edge detection is done very well and correctly if s0 is equal to the root mean square values of first derivatives.
Because a digital image often has locally blurred edges, only incomplete edges as shown in Figure 6 are generated by the above-mentioned processes. In order to generate successfully as complete edges as possible, we utilize a rule to link edge pixels. The rule is almost the same as the two principal properties used for establishing similarity of edge pixels in this kind of analysis. They are (1) the strength of the response of the gradient operator used to produce the edge pixel, and (2) the direction of the gradient that is often defined by tan-1(Gty/Gtx) ( Gonzalez and Woods, 1993). The detailed description about this rule will be published soon.
4. Test Results
Figure 6 shows some test results, where a blurred image of the Chinese character "dragon" is used as a test image. Its gradient image (Figure 6(b)) shows a complete but thick edges. In general, one concludes from these test results together with all of other tests that the Daubechies operator extracts edges with line width of about 2-3 pixels that is finer than the ones with line width of c.a. 4-5 pixels produced by the Sobel operator. Figure 6(c) shows apparently that the wavelet-based zero-crossing approach will produce some disjointed edges if no edge linking operation is done. Nevertheless, almost all disjointed edge center line segments are connected with each other very well if the edge linking operation is done after the zero-crossing approach is completed. Each edge has the width of 1 pixel. Figure 6(d) shows also some defects, e.g. incorrect edge linking exists in the right area. In contrast against that, Figure 7 shows another complete successful example. In short, an effective edge linking operation should be further studied.
Moreover, some 'noise-like' B-pixels (black edge pixels) shall appear, if a small threshold s0 (e.g. 0.05RMS) is used. RMS denotes the root mean square value of the derivatives. For example, wrong B-pixels appear on the lower right region of Figure 6(c).
 | |
| (a) | (b) |
 | |
| (c) | (d) |
Figure 6. an original image (a), its complete but thick edges represented by its gradient image computed by Daubechies operator of N=3 (b), disjointed thin edges produced by the wavelet-based zero-crossing approach without edge linking process (c), and complete and thin edges (edge width = 1pixel) produced by the proposed approach with edge linking operations, where there are some incorrectly linked edges.
 | |
| (a) | (b) |
 | |
| (c) | (d) |
Figure 7. an original image of the Chinese character 'honesty' (a), its gradient image computed by the Daubechies operator (b), its edge image produced by the wavelet-based zero-crossing approach without edge linking (c), and with the edge linking operations (d), where the Daubechies wavelet of order N=3 is used and edge linking is completely successfully done.
5. Conclusions
This paper presents a set of new symmetrical gradient operators. In this paper, they are named as "Daubechies operators". It is verified that the operators determined by the asymmetric Daubechies wavelets are the same with the ones determined by the least asymmetric Daubechies wavelets of the same order N. They provide alternatives for gradient computation. Test results show that they can extract much finer edges than the Sobel operators. The edge width is generally c.a. 2-3 pixels and 4-5 pixels, if edges are represented by first derivatives determined by the Daubechies operators and the Sobel operators, respectively. Moreover, the center lines of all edges determined by both Daubechies and Sobel operators are the same.
Disjointed edges are often generated in a blurred image. In order to generate successfully as complete edges as possible, the approach also utilizes a rule to link edge pixels. The rule adopts two principal properties: (1) the strength of the response of the gradient operator used to produce the edge pixels, and (2) the direction of the gradient. The detailed description about this rule will be published soon.
All tests show that the wavelet-based zero-crossing approach with edge linking operations is really available for edge extraction. It can produce successfully complete edges with a width of one pixel.
Preliminary tests show that there is no significant difference in those edges extracted by different order of Daubechies operators. Nevertheless, it should and will be further studied.
Incorrect edge linking often appears in locally blurred edges. An effective edge linking operation should be further studied.
The mathematical models and algorithms proposed in this paper can also be utilized to represent a general curve/line on a 2D plane or in a 3D space, e.g. see (Tsay, 2000). The concepts might and will be further extended to represent a multi-valued 3D surface.
Reference
- Daubechies, I., 1988. Orthonormal bases of compactly supported wavelets. Comm. Pure Appl. Math., 41, pp. 909-996.
- Daubechies, I., 1992. Ten Lectures on Wavelets. SIAM (=Society for Industrial and Applied Mathematics, Philadelphia, Pennsylvania, pp. 167-213.
- Gonzalez, R.C., and Woods, R.E,, 1993. Digital Image Processing. Addison Wesley, pp. 161-221 and pp. 414-443.
- Jawerth, B., and Sweldens, W., 1994. An Overview of Wavelet Based Multiresolution Analyses. SIAM Reviews, pp. 1-39.
- Mallat, S.G., 1989. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation. IEEE Transaction on Pattern Analysis and Machine Intelligence, Vol. 11, No. 7, pp. 674-693.
- Rioul, O., and Duhamel, P., 1992. Fast Algorithms for Discrete and Continuous Wavelets Transforms. IEEE Transactions on Information Theory, Vol. 38, No. 2, pp. 569-586.
- Tsay, J.R., 1996. Wavelets fuer das Facetten-Stereosehen. DGK (=Deutsche Geodaetische Kommission), Reihe C, Dissertation, Heft No. 454, Munich, Germany, pp. 53-57.
- Tsay, J.R., 1998. A New Algorithm for Surface Determination Based on Wavelets and its Practical Application. PE&RS, Vol. 64, No. 12, pp. 1179-1188.
- Tsay, J.R., 2000. DWT-based representation of a multi-valued line function. To be presented in the Technical University Darmstadt, Germany.
- Vetterli, M., and Kovacevic, J., 1995. Wavelets and Subband Coding. Prentice Hall, pp. 20-25.