| GISdevelopment.net ---> AARS ---> ACRS 1995 ---> Poster Session 4 |
A New and Efficient Transform
for Signal Processing Based on Gabor Discrete Disctete Cosine Transform
V.K. Singh, A.S.
Manjunath
National Remote Sensing Agency, Hyderabad, India
Abstract National Remote Sensing Agency, Hyderabad, India
Gabor transform is very useful for remote sensing applications. Since the Gabor elementary functions are not mutually orthogonal, its implementation is time consuming. The computational speed can be improved by using a modified transform, Gabor Discrete Cosine Transform (DCT), because of a real valued transform. The Gabor DCT was implemented for the purpose of image data compression for browse application in remote sensing area. Since this application needs time valued processing of the remotely sensed data, the speed achieved in implementation of Gabor DCT was not satisfactory. To achieve a higher throughput a new transform which is variant of the basic Gabor DCT has been developed. The paper discusses the new algorithm and implementation methodology. A matrix multiplication based method for computing new transform for any discrete signal images by both techniques are presented. The paper describes the new algorithm and implementation methodology.
Introduction
Remote sensing has been an efficient and useful technique for the monitoring and management of natural resources. Remote sensing involves acquisition, processing, analysis and archival of images acquired from airborne/ spaceborne platform. The Gabor Transform has been found to be vary useful for image analysis and compression tasks. Implementation of Gabor transform is very complicated and time consuming because the Gabor elementary functions are a set of overlapping functions and not mutually orthogonal. An important property of Gabor elementary functions is their achievement of the theoretical lower bound of joint un-certainty in the two conjoint domains, space and frequency (1). They achieve the maximum possible joint resolution in the conjoint visual space and spatial frequency domain. Furthermore experimental results show that the receptive field of the mammalian visual cortex can be very well represented using 2-D Gabor elementary functions. Some properties of the visual system, such as spatial localization, orientation selectivity and spatial frequency selectivity can also be modeled in terms of these functions (3).. Another important reason that encourages the user of Gabor functions is that it has been shown that the Gabor decomposition reduces the low-order entropy of the data (3). This means that, like DCT, the Gabor transform has the beneficial property of decorrelation. Therefore when the Gabor transform is used for image compression, in which the properties of the visual system can be incorporated into an image coding scheme, a high data compression ratio may be achieved.
Derivation of key formulae of Gabor representation is usually facilitated by relationships taken from Fourier and zak transform theory. Several of these fundamental formulas can be obtained directly using Bessel's equality (5). Complete discrete 2-D Gabor transforms for image analysis and compression was described by J.G. Daugman (3). Numerical implementation of the generalized Gabor expansions and synthesis was described by J. Waxler et al (4).
A very fast and easily implemented method was proposed by T. Ebrahimi and M. Kunt (6) for the computation of the weighting factors of the Gabor decomposition. A modified Gabor transform referred to as the Gabor DCT was proposed by Wang and Yan (B). An adaptive Gabor DCT was also proposed by H. Wang and H. Yan (2). An FET based gradient descent approach for fast implementation of the discrete 2-D Gabor transform was described by V. Srinivas et al (7).
Based on Gabor DCT, a new and efficient transform is proposed in this paper for discrete signal processing. The implementation of this transform and the results of both (Gabor DCT and New Transform) the transforms have been discussed. The weighting factors (6) are extracted by simple multiplication between a matrix and the vector data. Images are reconstructed by multiplying the matrix of the transform functions and vector of the weighting factors. The advantage of this transform is that, similar to Gabor DCT, the transformed coefficients of this new transform have more compact energy distribution than those of the Gabor Transform coefficient (1) and in addition, the computation speed of this transform coefficient (1) and in addition, the computation speed of this transform is much higher than that of the Gabor DCT.
2. Implementation of the new transform
2.1 The 1-D Transform
The one dimensional (1-D) discrete Gabor DCT elementary function (8) may be expressed as :
Where x0 represents a sample in the space domain, uo represents a sample in the spatial frequency domain and is spatial offset of the frequency modulation function. The Gabor DCT is calculated within area of support (defined by a) of Gaussian function, where x0 corresponds to the center of a Gaussian function.
Since the exponential and cosine functions are inter-related, a study was carried over in this regard and the Gabor DCT in (1) was modified and a new transform has been developed as:
Expansion of a discrete signal F(x) in terms of elementary functions of this new transform can be expressed as :
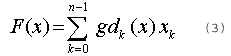
where xk are transform expansions. The above expression can be described in matrix notation (6) as :F=G.X
where
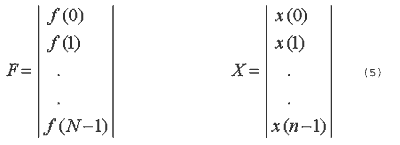
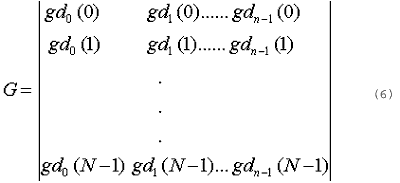
Solution of (4)can be found analytically [6] as:
Where
The original signal f (x), specified. say, at N points, is divided into block of dimension p, with centers located at {x} = {mp}for blocks m. The elementary functions, whose widths are determined by Gaussian envelop parameter in (3). are defined over a 2p spatial cell. a complete set of elementary functions of transform is defined for each block m by varying the spatial frequencies **corresponding to the 2p spatial cell. The parameter r takes on even integer values, r=0, 2, 4....... 2p-2, because the block size is p. The center of each elementary function coincides with that of a block and (2) can now b- rewritten as:
Each elementary function gdm,r is now uniquely determined by the integer m and r representing the spatial center and frequency parameter respectively [7]. we obtain n/p distinct values for m.
2.2 The 2-D Transform
In case of two dimensional (2-D) discrete Transform, the expansion of a 2-D discrete signal (for example an image) F (x,y) may be represented as:
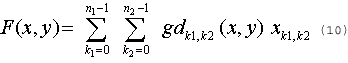
where x k1 are 2-D Transform expansions. Elementary functions gdk1 k2(x,y) are separable. They may be written as:
Here the Eq. (11) can be rewritten in matrix form as [6]:
Where
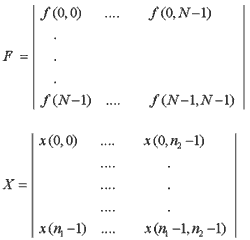
and G is same expansion matrix as described by Eq. (6). Solution of (10) can be found analytically (6) as :
where
Results and Discossions
Image compression is needed for browse application on remotely sensed data at NRSA, India. for this purpose, it was found that Gabor DCT is a suitable technique and the necessary software was developed to implement the same. After a comprehensive study to improve computational speed another useful variant Gabor DCT which we call here New Transform has been developed. Software for implementation of the New Transform has also been developed as already described. The software is developed in 'C' on Unix platform (SUN workstation) and performances of both the transforms have been measured. The software computes number of transform expansions based on same Mean Square Error (MSE) for both the transforms and then each expansion is coded in B bits. Both the techniques ware applied to picture and remotely sensed data of different sizes viz 256x256, 512x512 and 1k x 1k pixels. Performance measurement is made on the basis of MSE, compression ratio and computational speed. The MSE is computed between original and reconstructed images. Fig. (1) shows the original image whereas Fig. (2) & (3) show the reconstructed images using Gabor DCT and New Transform techniques respectively.

Figure 1 Original Image

Figure 2 Reconstructed Image using Gabor Dct compression Rate : 0.25 Bits/Pixel

Figure 3 Reconstructed Image using New Transform Compression Rate " 0.20 Bits/Pixel
At NRSA, several images of different sizes were compressed using both the techniques viz Gabor DCT and New Transform and our observations are shown in Table (1) and Table (2). It is observed from both the tables that for the same MSE the New Transform gives better compression ratio and the same time takes lesser time for computation. Quality of the compressed image depends upon number of transform expansions stored for that image. If number of transform expansions increases, quality of compressed image also increases i.e. MSE is reduced but the execution increases.
| Sl. No. | MSE | Compression Ratio (bits/pixel) | Execution Time (in sec.) | Image Size |
| 1 | 5.28 | 0.5 | 7.9 | 256x256 |
| 2 | 9.08 | 0.5 | 75.6 | 512x512 |
| 3 | 9.53 | 0.5 | 681.4 | kx1k |
| 4 | 10.11 | 0.125 | 3.3 | 256x256 |
| 5 | 17.65 | 0.25 | 29.0 | 512x512 |
| 6 | 19.02 | 0.25 | 276.7 | 1k x 1k |
| Sl. No. | MSE | Compression Ratio (bits/pixel) | Execution Time (in sec.) | Image Size |
| 1 | 5.28 | 0.4 | 7.7 | 25x256 |
| 2 | 9.08 | 0.4 | 72.8 | 512x512 |
| 3 | 9.53 | 0.4 | 632.4 | kx1k |
| 4 | 10.11 | 0.25 | 3.2 | 256x256 |
| 5 | 17.65 | 0.25 | 28.1 | 512x512 |
| 6 | 19.02 | 0.25 | 240.6 | 1k x 1k |
4. Conclustions
Gobor DCT and New Transform have been applied on 2-D discrete signals, such as remotely sensed images, and performances of both have been examined. It has been found that the computational speed achieved here for implementing this New non-orthogonal transform is quite satisfactory and it is suitable for various applications, such as image analysis, segmentation and compression, in remote sensing. It is observed that performance of New Transform is much better than the Gabor DCT. Since, like the Gabor DCT, transform coefficients of New Transform have a more compact energy distribution, a better image compression result can be achieved. The 2-D New Transform is also useful for image analysis and segmentation because, it also extracts locally windowed 2-D spectral information concerning form and texture without sacrificing information about 2-D location or more global spatial relationships.
References
- Hang Wang, Hong Yan, "Efficient image coding method based on adaptive Gabor discrete cosine transforms", Journal of Electronic Imaging, January 1993, Vol.2, No.1, pp. 38-43.
- H. Wang and H. Yan, "Adaptive Gabor discrete cosine transform for image compression". Electronics Letters, Aug. 1992, Vol.28, No. 18, pp. 1155-1756.
- John G. Daugman , "Complete discrete 2-D Gabors transforms by neural networks for image anlysis and compression". IEEE Trans. on ASSP. Vol.36, No.7, July 1988, pp 1169-1179.
- J. Wexler and S. Raz, "Discrete Gabor expansion". Signal processing, Vol.21, No.3, Nov. 1990, pp. 207-220.
- Richard H. Orr, "Derivation of Gabor transform relations using Bessel's equality". Signal Processing, Vol.30, No.2, January 1993, pp. 257-262.
- Touradj Ebrahimi, Murat Kunt, "Image compression by Gabor expansion". Optical Engineering, July 1991, Vol.30, No.7, pp. 873-880.
- V. Srinivasan, P. Bhatial and S.H. Ong, "A fast implementation of the discrete 2-D Gabor transform". Signal Processing, vol.31. No.2, March 1993, pp. 229-233.
- Wang H. and Yan H., "Efficient implementation of Gabor transform for image compression". Electronics letters, 1992, Vol.21, No. 9, pp. 870-871.